Problem wyznaczenia przestrzennego położenia źródła fal sejsmicznych jest jednym z podstawowych problemów sejsmologii. Ponieważ różne są wstrząsy sejsmiczne (naturalne, indukowane, duże, małe, itp) różne są też metody lokalizacji wstrząsów i nie ma jednej uniwersalnej metody którą można stosować w każdym wypadku. W niniejszym projekcie zajmujemy się zagadnieniami związanym z sejsmicznością indukowaną pracami górniczymi, głównie w głębokich kopalniach, więc i zagadnienie lokalizacji rozważane jest tu pod kątem typowych warunków występowania sejsmiczności indukowanej oraz warunków obserwacyjnych.
Klasyczne podejście do zagadnienia lokalizacji źródła sejsmicznego polega na sformułowaniu go jako zagadnienia optymalizacyjnego: szukamy takiego punktu w przestrzeni (zwykle ograniczamy się do wybranego fragmentu kopalni gdzie wstrząs był odczuty) dla którego modelowane czasy rejestracji fal przez seć sejsmiczną będą jak najbliższe wartościom zmierzonym. Metoda taka jest bardzo efektywna i szybka, jednakże nie pozwala w wiarygodny sposób ocenić dokładności otrzymanych wyników. Techniką bardziej zaawansowaną, pozbawioną powyższej wady jest technika oparta na metodach inwersji probabilistycznej. W tym podejściu nie szukamy "optymalnego" położenia ale konstruujemy rozkład prawdopodobieństwa (tzw. a posteriori) wyznaczający prawdopodobieństwo lokalizacji wstrząsu w danym punkcie. Metoda ta ma tylko jedną wadę – wymaga złożonych i czasochłonnych obliczeń. Jej praktyczne zastosowanie wymaga bowiem wyznaczenia prawdopodobieństwa a posteriori albo w węzłach regularnej siatki albo użycia zaawansowanych technik próbkowania probabilistycznego. Oba podejścia są na tyle wolne, że technika taka mimo swych ogromnych zalet nie może być stosowana rutynowo w kopalniach.
W ramach niniejszego projektu zaproponowaliśmy nowe podejście do problemu lokalizacji żródeł wstrząsów. Postanowiliśmy wykorzystać znaną z innych zastosowań metodykę Time Reversal. Opiera się ona na obserwacji, że równanie falowe opisujące propagację fal sejsmicznych posiada dwie ważne symetrie. Pierwsza z nich to symetria związana z zamianą ról źródła i odbiornika. Związana jest ona z faktem, że fale sejsmiczne, akustyczne itp. wyemitowane z punktu A i zarejestrowane w punkcie B wyglądają tak samo jak wymitowane z punktu B i rejestrowane w punkcie A pod warunkiem, że źródło fal było takie samo. Druga ze wspomnianych symetrii to symetria równania falowego względem odbicia czasu t → -t wynikająca z faktu, że w klasycznym równaniu falowym (bez członu tłumienia) występuje tylko parzysta pochodna czasowa. Wynikiem połączenia powyższych cech równania falowego jest technika inwersji akustycznego/sejsmicznego pola falowego zwanego time reverse miroring (TRM) . Polega ona na wstecznej w czasie propagacji zarejestrowanych przez odbiornik fal, które rozchodząc się w ośrodku, odbijając i interferując kolimują się w obszarze ich źródła. W ostatnich czasach próbuje się wykorzystać technikę TRM do analizy własności źródeł sejsmicznych.
Algorytm TRMLOC oparliśmy na uproszczonej wersji techniki TRM propagując wstecznie nie cały rejestrowany sejsmogram a tylko jego specyficzną charakterystykę: czas rejestracji pierwszej fali sejsmicznej (czas dotarcia frontu falowego do czujników). Ta własnie wielkość jest wystarczająca do lokalizacji źródła a równocześnie propagację wsteczną frontu falowego można przeprowadzić numerycznie bardzo łatwo i, co najważniejsze szybko. Wykorzystuje się tu fakt, że propagację frontu falowego opisuje równanie eikonalne które można rozwiązać szybko nowoczesnymi technikami takimi jak Fast Marching Method (FMA), Fast Sweeping Method (FSM) lub pochodnymi. Obydwie techniki, pozwalają wyznaczyć rozwój frontu falowego w całej przestrzeni a przez to automatycznie umożliwiają wyznaczenie rozkładu a posteriori pojawiającego się w kontekście inwersji probabilistycznej bez konieczności dodatkowych, czasochłonnych obliczeń. Ponieważ propagacja wsteczna zarejestrowanych czasów wejść fal musi być przeprowadzona dla wszystkich odbiorników, a odpowiadające obliczenia są całkowicie niezależna dla każdego z odbiorników proponowany algorytm jest "z natury" predysponowany do implementacji obliczeń równoległych co dodatkowo podnosi jego trakcyjność.
Poniżej przedstawiamy dwa przykłady zastosowania algorytmu TRMLOC do analizy wstrząsów zarejestrowanych przez hipotetyczną sieć sejsmiczną pracującą w obszarze około 10 x 10 km i umieszczoną na głębokości około 1000 m. pod powierzchnią ziemi.
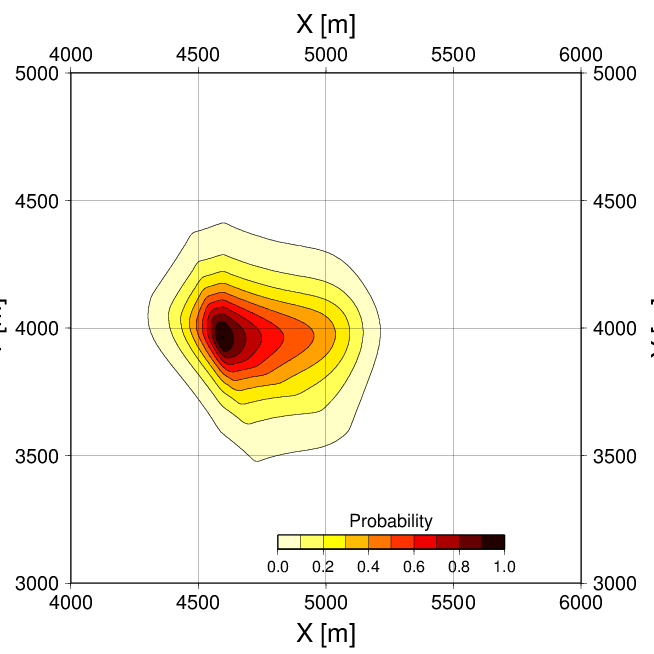
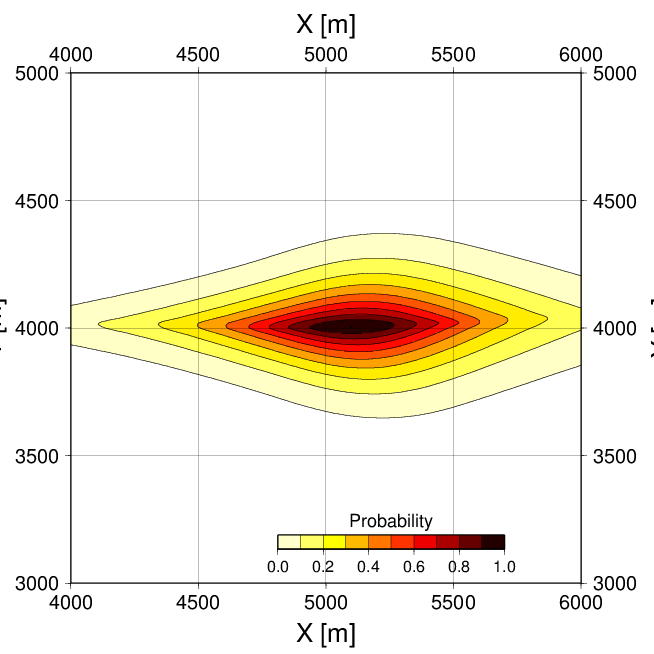
Pierwszy przykład (A) )dotyczy przykładowej sytuacji w której wstrząs został zarejestrowany przez 7 stacji praujących w odległościach do około 5 km od epicentrum wstrząsu. (wschód-zachód, północ - południe) pokazany jest na poniższym rysunku po lewej stronie. Drugi przykład (B), także syntetyczny, opisuje sytuację, gdy tylko dwie stacje zarejestrowały fale sejsmiczne. Ponieważ do wyznaczenia mamy trzy parametry spodziewamy się w takiej sytuacji, dużych błędów lub ogólniej, że któraś ze składowych lub ich kombinacje mogą być bardzo źle wyznaczone. Rozkłady a posteriori dla składowych epicentralnych położenia (X,Y) dla przypadków A (lewy rysunek) i B (prawy rysunek) pokazane są poniżej
 |
 |
| Przykład A | Przykład B |
Wstrząs A zlokalizowany jest dosyć dobrze z błedami lokalizacji (rozmiar ciemnego obszaru o dużym prawdopodobieństwie) około 50x50m. Oczywiście ptarząc na kształt powyższego rozkładu, widać, że przestrzenny rozkład błędów jest dosyć skomplikowany i niewiele będzie przypominał klasycznę elipsę błędów. W przykładzie B (prawy rysunek), doskonale widać, że składowa X jest bardzo niedokładnie określona a dane obserwacyjne pozwalają oszacować z rozsądną dokładnością jedynie składową Y położenia epicentrum wstrząsu.
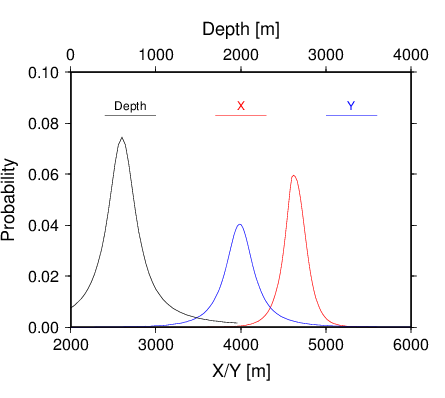
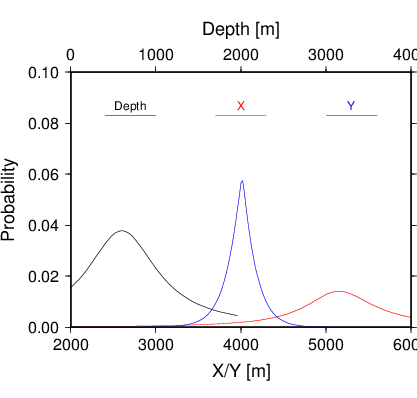
Dokładność wyznaczenia współrzędnych źródła wstrząsów najprościej oszacować na podstawie jednowymiarowych rozkładów brzegowych. Poniższe rysunki pokazują takie rozkłady dla powyższych przykładów.
 |
 |
| Przykład A | Przykład B |
W przykładzie A (lewy rysunek) błędy wyznaczenia wszystkich trzech składowych położenia źródła wstrząsu wyznaczone są z podobną dokładnością. W przypadku B (lewy rysunek) ) doskonale widać, że błędy wyznaczenia składowych X i Z są bardzo duże w tym przypadku – praktycznie składowe te są nieokreślone.
W niniejszej krótkiej prezentacji w sposób bardzo skrótowy i schematyczny opisaliśmy pierwsze wyniki testów syntetycznych nowo zaproponowanego algorytmu lokalizacyjnego. Wykonuje on pełną inwersję probabilistyczną przez co, jak demonstrują zamieszczone przykłady możliwa jest pełna ocena błędów otrzymanych rozwiązań. Równocześnie zaproponowany algorytm jest bardzo szybki. Czas obliczeń na 4-rdzeniowym procesorze I5 z dynamicznie zmienianym zegarem (800MHz – 2.4 GHz) wynosił około 30s. dla każdego z przypadków a osiągnięta teoretyczna dokładność lokalizacji wynikająca z rozmiarów siatki wynośiła 20m., a więc była bardzo wysoka.